We go through life and events happen to us which we categorise as either desirable or undesirable. As the saying goes, you win some and you lose some.
As people, it can feel natural to repeat actions that lead us to wins and conversely avoid actions that leads us to losses. But in a situation where we win or lose, how much of this result was due to our actions versus external factors outside of our control?
RNG vs G2 Worlds 2018 quarterfinals
This was an amazing upset where G2 eSports took down the Chinese powerhouse and tournament favourites RNG in a 5 game series.
According to G2’s captain Luka Perković the win was “definitely unexpected right?” (see his post game interview here) but just how unexpected was it?
From a narrative perspective, G2 was the 3rd best team from the 3rd best region and RNG was the best team from the best region. From that angle, the upset was colossal.
But what about from a statistical angle?
Flipping a coin
To understand the calculation behind the probability of G2’s series win, let’s use a contrived example of flipping a coin 5 times. Over our flipping, what is the probability that it lands heads three times and tails twice? We need 3 pieces of information to calculate this:
| Description | Explanation | |
|---|---|---|
| 1 | An assumption of independence between results. | Since the result of one flipped coin does not depend on the result of another, we can say these events are independent. This is a convenient statement because it means the probability of a set of results occurring is the probability of each individual result multiplied together. |
| 2 | The number of ways the entire result can occur. | The number of ways we can flip 3 heads and 2 tails is 10. |
| 3 | The likelihood of achieving the individual result. | The likelihood of flipping a head is 50%. |
So the probability of flipping heads 3 times and tails 2 times is (50% * 50% * 50%) * (50% * 50%) = 3.125%. But these heads and tails combinations can occur in 10 different ways so we have to multiply this number by 10 and we get a 31.25% chance of flipping 3 heads and 2 tails.
Probability of winning a series
In professional League of Legends a series is played over 5 individual games and the first team to win 3 games wins the series. G2 won their series against RNG with 3 wins and 2 losses but let’s just ask the question of winning a series in general. Using the same logic as before:
| Description | Explanation | |
|---|---|---|
| 1 | An assumption of independence between results. | Assuming independence is definitely an incorrect assumption since the previous game affects the next game in many ways (player mentality, draft, side selection etc). But let’s make it anyway so that we can carry on with the calculation. |
| 2 | The number of ways the entire result can occur. | There are 10 combinations that you can win a series. |
| 3 | The likelihood of achieving the individual result. | ??? |
Determining 3 is interesting.
For the coin example, we know that the probability of flipping a head is 50%. But what is the probability of G2 winning a game against RNG?
There’s no way to ever know. We know that G2 won a single series against RNG, but what does that tell us?
Graphs
Ok so we don’t know the likelihood of G2 beating RNG in a single game (or any team beating any other team in a game for that matter), but we do know that they won.
Let’s add The likelihood of achieving the individual result as a dimension, and graph the probability of winning a series for all values of an individual game win probability (0% - 100%).
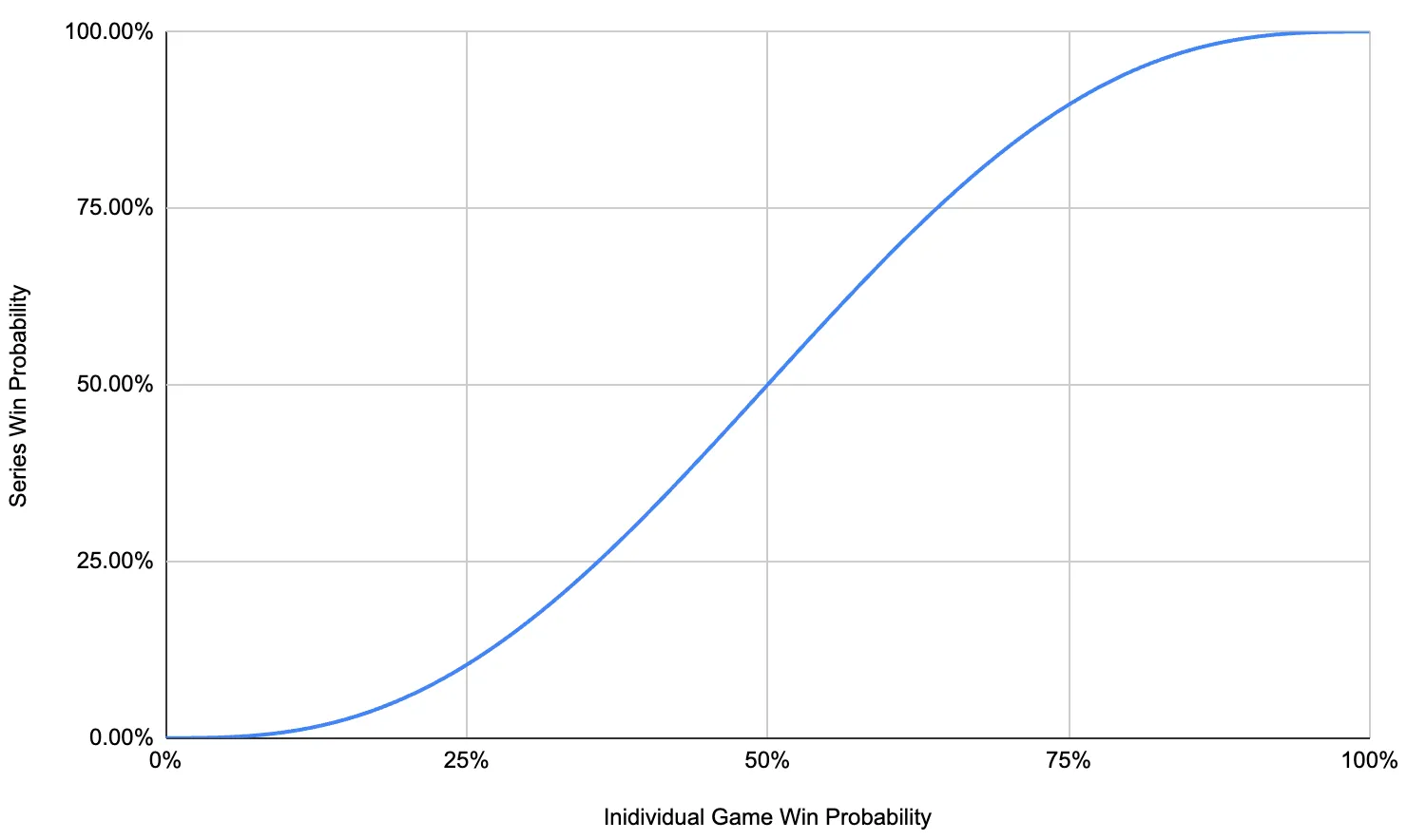
What is this graph saying?
If you’re a team with a 50% chance of beating your opponent in a single game, you have a 50% chance of beating that team in a series.
If you’re a team with 75% chance of beating your opponent in a single game, you have a 89.65% chance of beating that team in a series.
If you’re a team with 95% chance of beating your opponent in a single game, you have a 99.88% chance of beating that team in a series.
Ok so if my team wins a series against another team, what is the probability that I’m actually a better team? “A better team” meaning I have a higher individual game win rate greater than 50%?
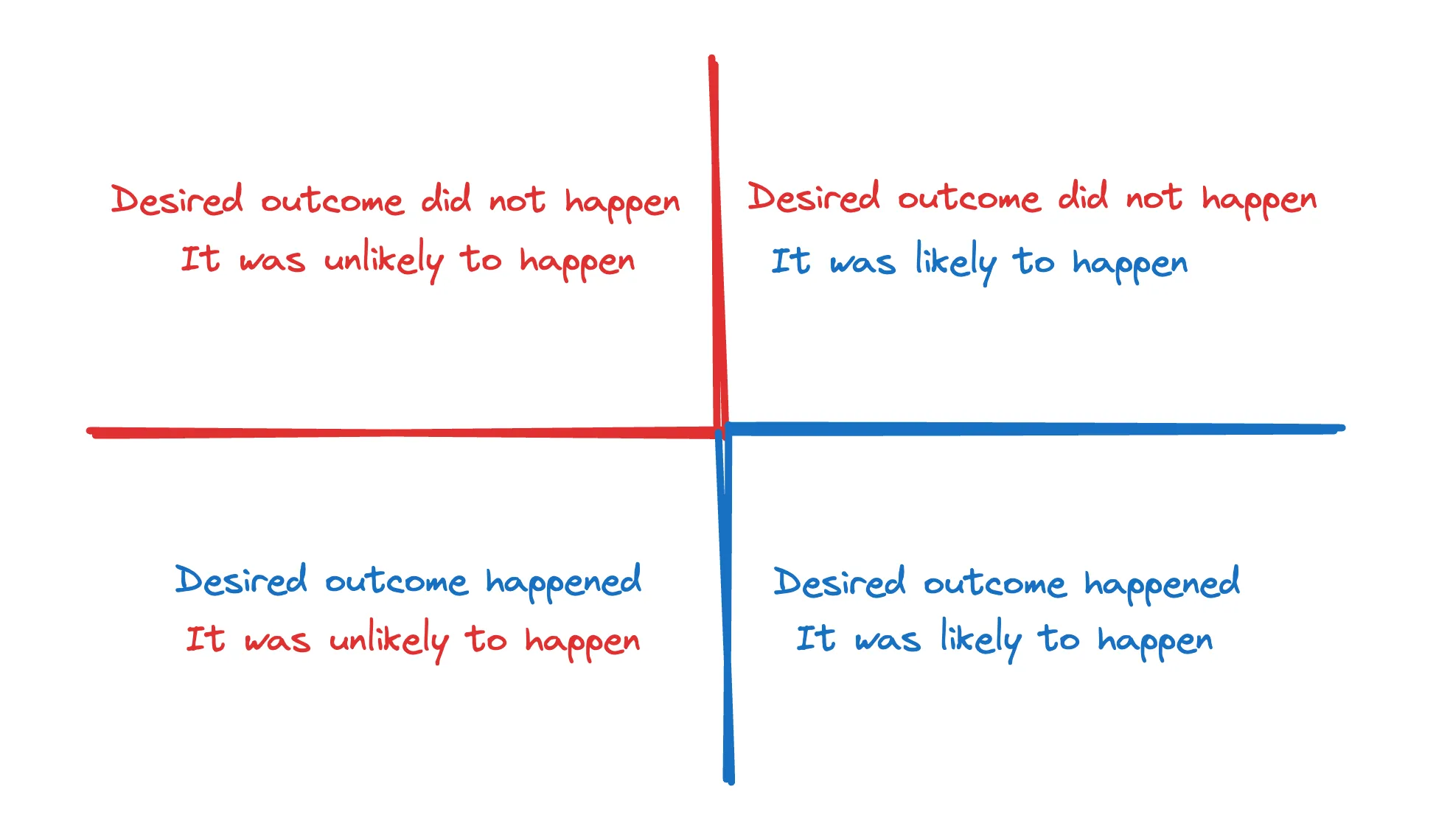
We can split up our graph into 4 sections:

- I won the series and I am a better team.
- I won the series but I am a worse team.
- I lost the series and I am a worse team.
- I lost the series but I am a better team.
The probability that I am a better team given I won a series can be calculated by, in English: The probability that I won the series and I am a better team, divided by the probability that I won a series (whether I was a better team or not).
Or as an equation:
P (Bbetter team | Wseries win) = P (Wseries win n Bbetter team) / P (Wseries win)1
So how do we know what these values are? The area of each section represents the probability of those 2 outcomes being true. Notice how the total area of the graph is 100% x 100% = 100%?
Let’s add some areas to our graph:

We’re interested in the blue shaded area divided by the blue + red shaded area:
P (Bbetter team | Wseries win) = 42.19% / (42.19% + 7.81%) = 84.38%
So if my team beats your team in a 5-game series, there is a 84.38% chance that my team was actually a better team. There is also a 15.62% chance that my team was worse than yours and I got lucky.
Or conversely, if my team loses a series, there is a 15.62% chance that my team was actually better than yours, we just got unlucky.
I’m not sure the fact that there’s still a 15.62% chance that they are a better team than G2 gives RNG any solace in their crushing defeat in 2018.
Real life
While talking about League of Legends is interesting, the 4 section graph actually exists for every outcome in your life! Drawn more generally:
The exact size and therefore probability of each section we cannot know, but we know that those possibilities exist.
“Congratulations you won a League of Legends series!”
“Congratulations you got that job promotion!”
“Congratulations that person you asked out said yes!”
Just because the outcome was desirable doesn’t mean the outcome was likely.
Just because the outcome was desirable doesn’t mean you did the right things to achieve that outcome.
There is always the possibility that you got lucky. There will always be the possibility that you are in that bottom left quadrant.
Let’s talk about luck
What does it mean to get lucky or unlucky?
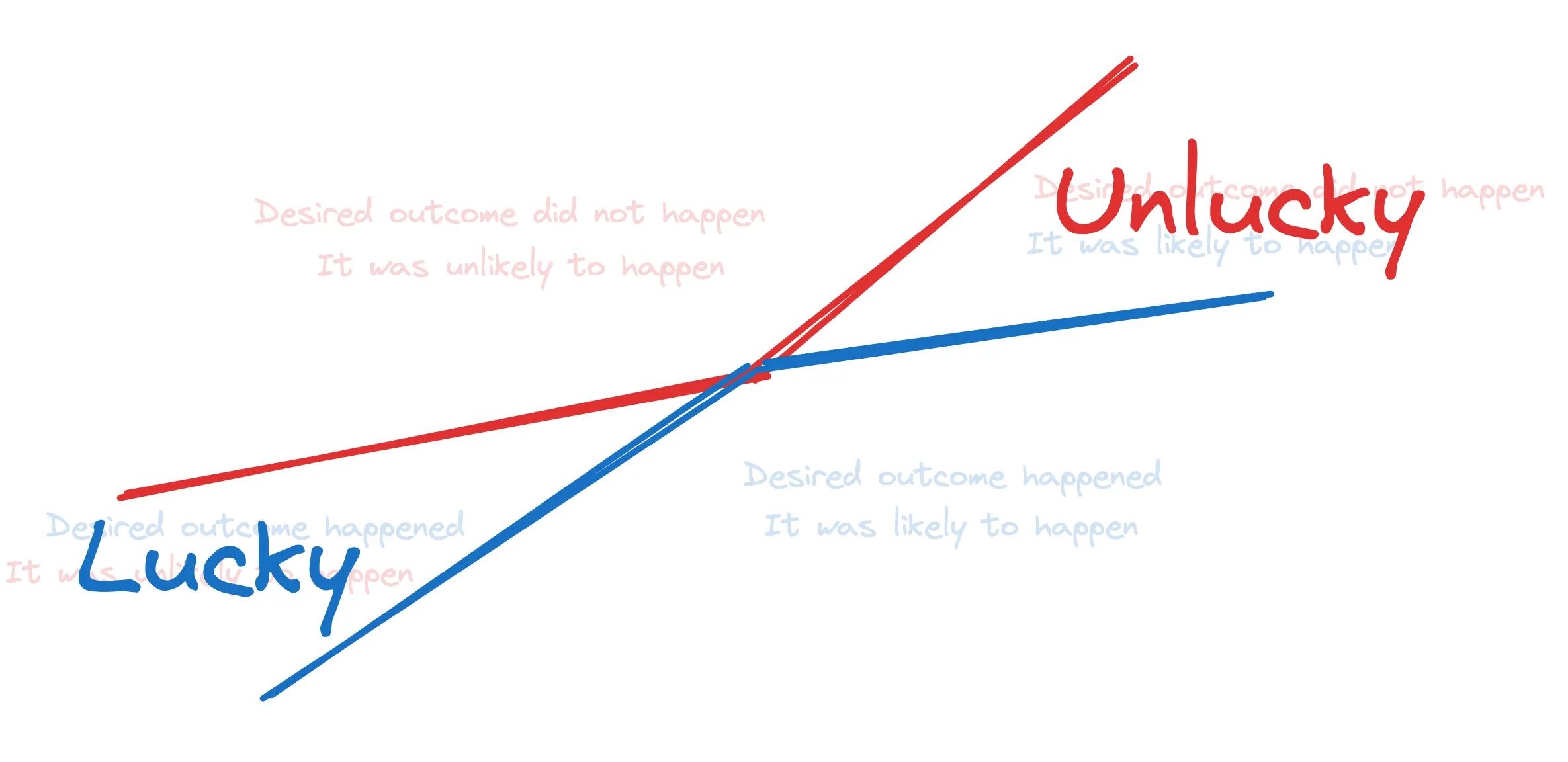
In terms of these quadrants, we are talking about the top right and bottom left:
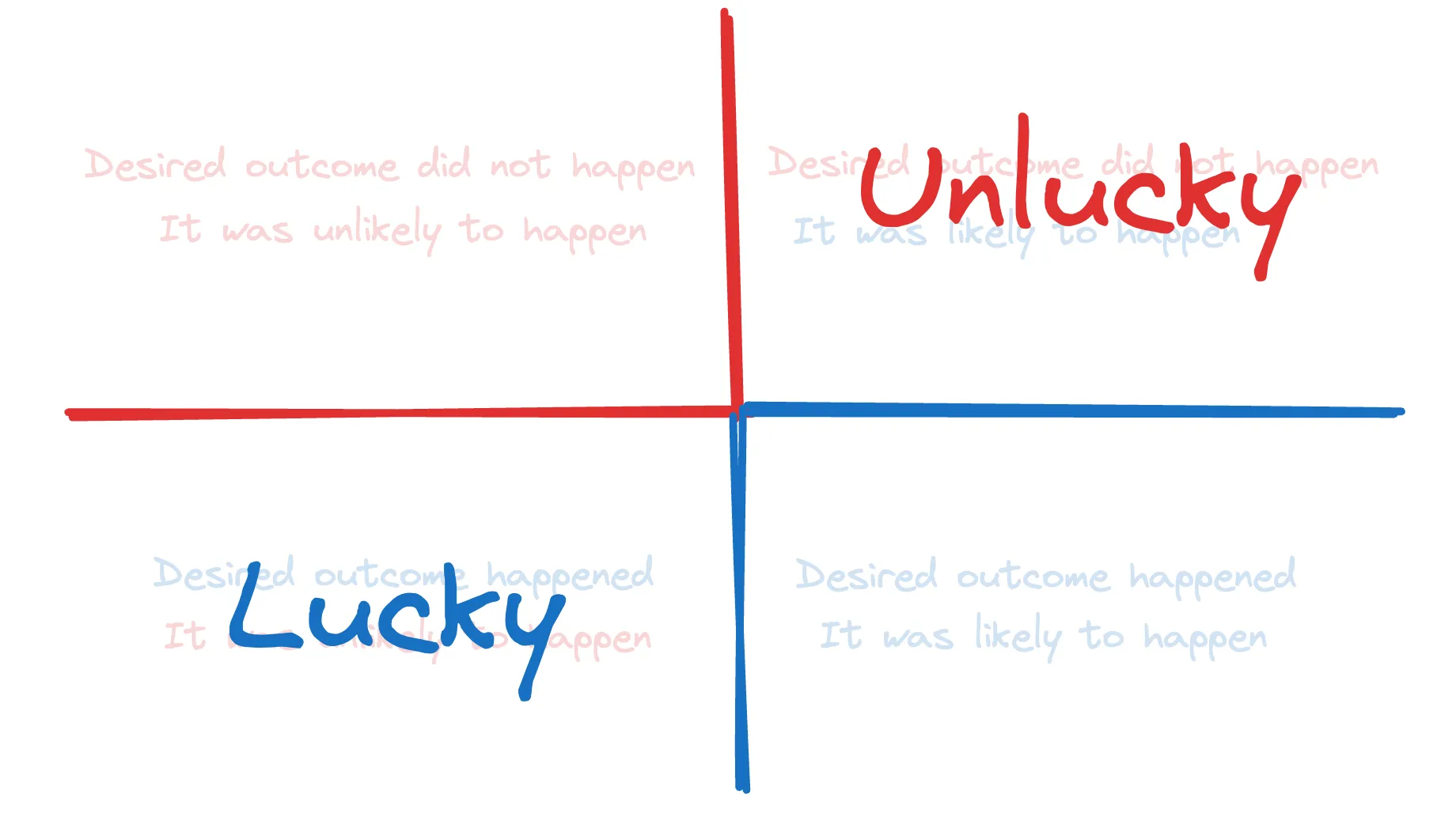
An example of getting unlucky
Let’s say you’re applying for a job and so the desired outcome is that you receive an offer. It’s important in a job interview to leave a good impression and let’s assume an effective way to do that is to tell a joke. This isn’t necessarily true, but let’s assume it for this example.
Now let’s say the interviewer hates jokes. It doesn’t matter how funny the joke is, they hate jokes. Being the funny person that you are (and knowing that this is generally an effective strategy to succeeding in job interviews), you open the interview with a funny, witty and innocent joke.
When the interviewer denies you because they hate jokes, people might say “ah well, you just got unlucky”.
You’re in the top right quadrant.
Does that mean telling a joke at the start of an interview is universally bad? Does that mean you should change your entire strategy just because of 1 bad outcome?
An example of getting lucky
Let’s say you’re playing a game of Aussie Rules football. You’re less than a goal down and you’re lining up a kick for the win. Unbeknownst to you, a big gust of wind is about to hit the oval at the exact moment you kick the ball and correct the slight right veer that you always have in your kicks. The ball goes in and your team wins.
Everyone cheers and your team is forever grateful. Wow, that was such an impressive kick! they proclaim. I can’t believe you actually kicked it! they cheer.
Now, had the gust of wind not arrived with that exact speed in that exact direction at that exact time, you would have missed. You were not across the local area’s weather patterns during the game and did not factor this into your kick. You are in the bottom left quadrant.
It’s a but unreasonable to expect that you should have known about the gust of wind, but you could have known it. Does that mean the gust of wind was only considered a piece of luck because I didn’t know it? What if someone else was taking the kick and they did know about it? Would it still be considered luck when the gust of wind knocks their ball in? Is luck just a lack of information? If so, can luck be relative?
Is luck just a lack of information?
While it’s unreasonably to expect that you know everything about your interviewer or the exact wind patterns during your game, that is information that you could have known.
It’s only a source of randomness because you didn’t know it.
As you develop your skills and become an expert, you are reducing the size of those luck-based quadrants. This is where the saying “you create your own luck” comes from.
So how small can they get? Can the be 0?
Luck always has a role
Even in some theoretical situation where you know absolutely everything, the universe has randomness baked into it (read about this here).
So while those luck-based quadrants can be really small, they will never be 0.
Luck always has a role.
Takeaways
If luck is some inevitable ingredient mixed into our recipes that always changes the flavour, so what? How does this change my life?
People will often look at one outcome that an individual achieves and think “damn, I wish I did what they did.” But as we have learnt, it’s difficult to know whether they achieved the outcome because of the steps they took, or whether some random events pushed them over the line?
Did I not get the job because the interviewer is a grim, un-joyous person who dislikes all forms of happiness, or maybe I’m just not funny?
Did I kick the winning goal for my team because I’m an absolute mega-chad who is the best player to touch the game, or did the wind help me out?
Did G2 really employ better strategies than RNG and outplay them around the map or did they catch RNG unprepared and win a couple of key moments throughout the series?
It’s a bit of both.
You can never know exactly how much of a role luck played but you can be certain that it did.
This fact should make you more forgiving of your mistakes, less envious of other’s successes and less egotistical towards life; despite “your” successes, you probably lucked out for most of them.
If you have repeated successes or repeated failures, then perhaps you have reason to dive deeper into your strategy. But otherwise, you win some and you lose some.
Footnotes
-
Yes this is Bayes’ Theorem. ↩